

And the total number of nodes in h levels is 2 h-1. If we number the levels tree from 1 to h, the level with index i can have up to 2 i-1 nodes. If h=4, we can add up to 8 more nodes, for a total of n=15.īy now you might see the pattern. If h=3, we can add up to 4 more nodes, for a total of n=7. If h=2, we can add two more nodes, for a total of n=3. If h=1, the tree only contains one node, so n=1. So what can we say about the relationship between the height of the tree, h, and the number of nodes, n? Starting small and working up: In general, the number of comparisons is proportional to the height of the tree, not the number of keys in the tree. In this example, it takes 4 comparisons to find the target, even though the tree contains 9 keys. And then you find the key you are looking for. Because target is less than 6, you go left. Because target is greater than 3 you go right. Because target is less than 8, you go left. For example, if you look for target = 4 in the previous diagram, you start at the root, which contains the key 8. If there isn't one, target is not in the tree.Īt each level of the tree, you only have to search one child. If target is greater than the current key, search the right tree. If there isn't one, target is not in the tree. If target is less than the current key, search the left tree. Starting at the root, we can use the following algorithm:Ĭompare the key you are looking for, target, to the key in the current node. Looking up a key in a binary search tree is fast because we don't have to search the entire tree. You can also check that the other nodes have this property. The key in the root is 8, and you can confirm that all keys to the left of the root are less than 8, and all keys to the right are greater.

This figure is from the Wikipedia page on binary search trees, which you might find useful while you work on this lab. The following diagram shows a tree of integers that has this property. If node has a right child, all keys in the right subtree must be greater than the key in node.If node has a left child, all keys in the left subtree must be less than the key in node.Binary search treeĪ binary search tree (BST) is a tree where each node contains a key, and every node has the "BST property": Along the way, we'll analyze the performance of the core map methods when implemented using a tree. In this lab, we'll explain how binary search trees work and then you will use one to implement a Map. Inside the TreeMap, the keys are not stored in order they are stored in a binary search tree, which makes it possible to traverse the keys, in order, in linear time. Instead of constant time, a TreeMap takes time proportional to log n. The order of growth is not quite as good.
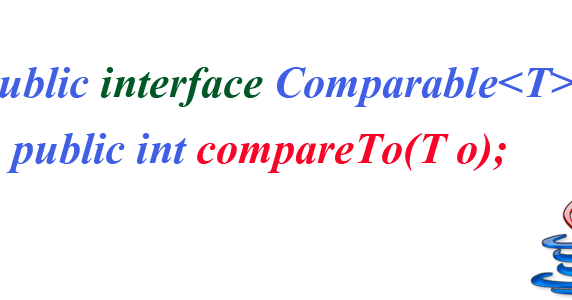
It turns out to be hard to solve both of these problems at the same time, but Java provides an implementation called TreeMap that comes close: For some applications, it is necessary, or at least useful, to keep the keys in order. The keys in a hash table are not stored in any particular order in fact, the order might change when the table grows and the keys are rehashed.

Hashing can be slow, so even though HashMap operations are constant time, the "constant" might be big. There are two reasons you might want another implementation: And by making your own Map using a hash table, you should understand how HashMap works and why we expect its core methods to be constant time.īecause of this performance, HashMap is widely used, but it is not the only implementation of Map. Analyze the performance of a tree-backed map.Īt this point you should be familiar with the Map interface and the HashMap implementation provided by Java.Implement the Map interface using a binary search tree.


 0 kommentar(er)
0 kommentar(er)
